Frustum Traced Shadow With Irrelgular Z Buffer 0

Percentage-Closer Filtering Shadows 에서 PCF 를 응용한 PCSS 라는 Soft Shadow 를 나타내는 기법에 대해서 알아보았다. 이번 글에서는 여태까지 알아본 것들에 비해 굉장히 최근에 나온 기법인 frustum-Traced Shadow 에 대해서 알아볼것이다.

해당 기법은 2015년에 Siggraph, Interactive 3D 같은 컨퍼런스에서 발표되었으며, 현재 Tom Clansy’s the Division 에 PCSS 와 혼합된 형태(Hybrid frustum Traced Shadow)로 적용되어 있다. Frame Rate 에 조금 영향을 미쳐 대부분의 게이머들은 아직은 HFTS 를 사용하지 않는듯 하다.(Reddit : Nvidia HFTS (The Division)) 하지만 컴퓨팅 파워가 늘어나는 것을 가정한다면 앞으로 하이엔드 게임의 주 옵션이 될수도 있겠다.

이 기법의 저자는 Shadow Map 처럼 따로 붙은 기법없이 Aliasing 이 없어야 했으며, 현세대의 GPU 와 해상도를 Interactive 하게 지원하는 것이 완벽한 Hard Shadow 를 목표로 FTS 를 고안했다. 가장 많이 쓰이는 Shadow Map 기법은 공간적(Light-Space 와 Clipping-Space 의 Discretize 된 결과의 차이), 일시적인(필터링이 필요한 Aliasing)인 문제들이 산재한다. 이는 이 기법을 고안한 시발점이였다.

FTS 의 이론적인 뿌리를 정하기 위해 저자는 여태까지 존재하는 여러 기법을 언급한다. 빛을 하나의 직선단위로 시뮬레이팅 하는 Ray-Tracing, 볼륨을 통한 각각의 폴리곤들을 테스트 하는 Shadow Volume, Irregular Z-Buffers 를 언급했다.

Shadow Volume 은 3차원상으로 Shadow 가 생기는 부분을 정해 그 부분을 테스트해서 Shadow 를 정해주는 기법이다. 이는 Shadow Map 보다 픽셀 단위로 처리할 수 있지만, 여러 단점이 있다고 한다. 한번에 해결되는 깔끔한 방법이 없으며, 보이지 않는 부분도 처리하기 때문에 Fill-Rate 를 많이 소모한다. 게다가 처리 자체가 간단하지 않기 때문에 개발자들도 많이 쓰는 기법이 아니라고 한다. 필자도 Shadow Map 에 대한 자료는 굉장히 많이 봤지만 Shadow Volume 은 거의 본적이 없다.

Ray-Tracing 은 빛을 직선 단위로 시뮬레이팅을 하는 기법으로, 계산 비용 자체가 비싸기 때문에 하드웨어와 구조에 굉장히 의존적이라고 한다. 게임에서도 쓰일 수 있는 기법이 있었지만 다른 후보에 밀려났다. 바로 Irregular Z-Buffer 다. 현대 GPU 의 Geometry -> Rasterize 구조에 맞춰 가장 걸맞는 방법이라고 한다. 자세한 설명은 아래에서 보자.

Key Idea

이 기법의 중요한 아이디어는 앞에서 소개한 Irregular Z-Buffer 와 frustum-Triangle Test 이 두가지다. Irregular Z-Buffer 는 앞서 Shadow Map 의 단점중에 공간적 괴리를 해결하는 데이터 구조이고, frustum-Triangle Test 는 논문에서 한 말을 이용하면 Sub-Pixel Accurate Pixel 을 구성하기 위한 시뮬레이션 테스트다. 이 두가지를 간단하게 살펴보자.

첫번째로는 바로 위에서 언급했던 Irregular Z-Buffer 다. 여기서의 IZB 는 우리가 알던 일반적인 Buffer 의 쓰임새와는 조금 다르게 쓰인다. 이 기법에서의 IZB 는 일반적인 Shadow Map 에서의 Eye-Space 와 Light-Space 의 괴리를 없에기 위해 Light-Space 를 기준으로 Depth 를 쭉 저장하는게 아닌, Eye-Space 의 각각 픽셀별로 표현하는 물체에 영향을 미치는 광원을 방향으로 Ray 를 쏜다. 그리고 Light-Space 를 기준으로 만든 Grid 버퍼에 Ray 가 부딫치고, 부딫친 부분에서 가장 가까운 텍셀에 데이터를 저장한다. 위에서 설명한 IZB 를 구성하는 방법에 대한 그림이 아래에 있다.

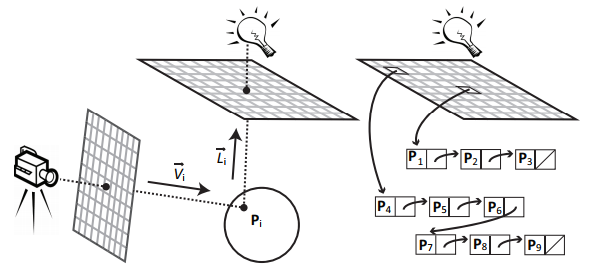
간단하게 이런식으로 IZB 가 구성되는 것을 알 수 있다. 이제 Geometry 와 비교하는 Visibility Test 가 필요하다. 일반적인 Shadow Mapping 의 Visibility Test 와는 조금 다르다. 기존의 Shadow Mapping 은 정점을 Light-Space 로 바꾸어 Z 값을 비교하여 Visibility Test 를 한다. 하지만 이 기법에서의 Visibility Test 는 다르다. 위에서 언급한 것과 같이 IZB 를 만든다. 그 다음 Occlluder Geometry 들을 Light-Space 를 기준으로 Conservative Rasterization 을 해준다.¹ 그렇게 나온 결과를 통해 IZB 와 함께 Visibility Test 를 한다. Conservative Rasterization 의 결과는 거의 Flag 로 사용될것으로 예측되고, Eye-Space 픽셀의 그림자 계산은 복잡한 계산을 통해 구한다. 아래는 논문에 있던 IZB 를 기준으로 쓰여진 수도 코드다.

// Step 1: Identify pixel locations we need to shadow
G(x, y) ← RenderGBufferFromEye()

// Step 2: Add pixels to our light-space IZB data structure
for pixel p ∈ G(x, y) do
    lsTexelp ← ShadowMapXform[ GetEyeSpacePos( p ) ]
    izbNodep ← CreateIZBNode[ p ]
    AddNodeToLightSpaceList[ lsTexelp, izbNodep ]
end for

// Step 3: Test each triangle with pixels in lists it covers
for tri t ∈ SceneTriangles do
    for frag f ∈ ConservateLightSpaceRaster( t ) do
        lsTexelf ← FragmentLocationInRasterGrid[ f ]
        for node n ∈ IZBNodeList( lsTexelf ) do
            p ← GetEyeSpacePixel( n )
            visMask[p] = visMask[p] | TestVisibility[ p, t ]
        end for
    end for
end for

다음은 Visibility Test 다. 논문에서는 frustum-Triangle Test 라고 부르는데, 이는 조금 복잡한 과정으로 구성된다. 아래 그림을 보면서 알아보자.

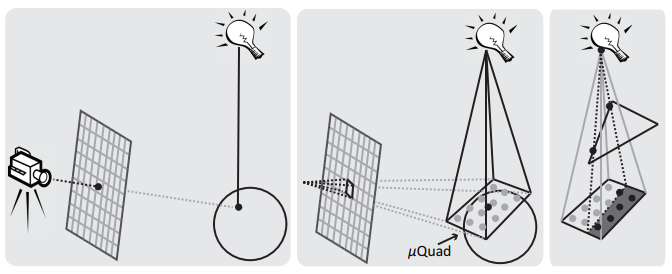
가장 처음에는 μQuad 라는 것을 생성한다. μQuad 는 Tangent-Space 를 기준으로 설정하며 각 픽셀별로 생성한다. 위 그림에서는 중간 그림에 구 위에있는 평면을 뜻한다. 그 다음 가리는 Geometry 의 폴리곤들의 각각의 Edge 를 사용하여 Shadow Plane 을 생성한다. 마지막으로 만들어진 Shadow Plane 을 μQuad 에 Projection 한다. 이때 가지고 있던 LUT 를 통해 가려짐을 계산한다. 그리고 다른 Edge 들도 계속해서 누적시킨다.

간단하게 frustum-Triangle Test 의 단계에 대해 설명해보았다. 이제 각각의 과정 : μQuad Construction, Shadow Plane Construction, Visibility Computation 에 대해 조금 더 자세히 써보겠다.

μQuad 의 생성은 Geometry 의 Tangent-Space 를 기준으로 계산되는 것 빼고는 특이한 점이 없다. 하지만 생성되는 시기에 대해선 조금 특별한게 있다. 가시성을 계산할 때 생성할 수도 있지만 G-Buffer 를 생성할 때 미리 계산하는 것이 더 효율적이라고 한다.

가시성을 계산할 때 ray-triangle intersection 을 계산하기 보다는 앖에서 언급한 각각의 폴리곤의 Shadow Volume 을 각 점마다 계산한다고 한다. Shadow Volume 은 그림자를 생성하는 Occluder Triangle 을 기준으로 각각의 Edge 에서 뻗어나오는 직사각형 면으로 구성된다. 아래 그림을 보면 쉽게 이해할 수 있다. 그리고 μQuad 에서 샘플링한 각각의 점들을 기준으로 가시성을 계산한다면 한다면, 4번의 내적으로 가시성을 테스트할 수 있다는 것을 의미한다.

또한 그림자를 멀티샘플링 하기 위해서는 여기서 언급한 Shadow Volume 의 Shadow Plane 들을 이용한다고 한다.

마지막으로 Visibility Computation 이 남아있다. 이 부분의 대략적인 것은 위에서 언급했다. 자세한 계산방식을 말해보겠다. 위에서 언급한 μQuad 와 Shadow Plane 사용해서 해당 폴리곤들의 데이터 누적을 위해서는 μQuad 에서 이산화된 binary 샘플링이 필요하다. 논문의 저자는 32 번의 Halton sampling² 을 사용했다고 한다.

가시성을 계산하기 위해서는 Shadow Plane 을 μQuad 에 Projection 해줘야 한다. 그러면 μQuad 는 최대 3개의 line 을 얻게 된다. 논문에서는 이 line 을 μQuad 를 기준으로 극좌표계³ 데이터로 저장한다고 한다. 반지름과 각도가 5bit 크기로 저장된다. 해당 10bit 데이터를 사용하여 미리 계산된 테이블에서 32개의 이진 가시성 샘플을 가져온다. 결과와 bit 단위의 and 연산을 통해 μQuad 의 가시성을 계산할 수 있다고 한다.

해당 기법을 고안한 사람은 두가지의 아이디어 : Irregular Z-Buffer 와 frustum-Triangle Test 를 통해 Sub-pixel Hard Shadow 의 이론을 만들었다. 하지만 이 아이디어들과 구현을 위한 노력의 차이는 꽤 큰듯하다. 논문을 보면 아이디어에 대한 텍스트보다 최적화를 위한 텍스트가 2배가 될정도로 많다. 다음 글에서는 논문에서 나온 전체 과정과 디테일한 구현 사항에 대해 적어보겠다.

참조

• Frustum-Traced Irregular Z-Buffers: Fast, Sub-pixel Accurate Hard Shadows
• Wikipedia : Irregular Z-Buffer
• cywman.org : HFTS Presentation Video
• NVidia : Don’t be conservative with Conservative Rasterization
• NVidia : Advanced Geometrically Correct Shadows for Modern Game Engines