Opaque As Alpha Test
Shader 에서 샘플링하는 Texutre 에서 Alpha 값을 가지고 있어, Alpha 을 참조해서 실제 픽셀에 출력을 하는지 안하는지를 결정하는 것을 Alpha Test 라고 한다. 이런 Material 이나 Texture 를 Cutout 이라고 통칭하는 경우가 많다.
보통 게임에서의 Alpha Test 를 사용하는 것들은 나무, 풀 같은 식생들(Vegetation)이 있고, 중간에 구멍이 뚫린 펜스같은 것들도 존재한다. 자연을 배경으로하는 게임의 경우에는 식생들이 굉장히 많기 때문에 Alpha Test 를 사용하는 Shader 가 굉장히 많이 사용될 것이다.

하지만 Alpha Test 는 굉장히 큰 단점이 있다. 고정된 화면 해상도에서 물체가 작게 표현되면 물체를 표현할 수 있는 픽셀의 숫자가 많이 작아진다. 물체를 표현하는 픽셀의 수가 작아지게 되면 일반적으로 해당 넓이에 맞게 생성된 Texture 의 Mip-level 에 접근한다. 중간의 Alpha Test 그림을 보면된다.

실제로는 양 옆의 물체들처럼 자연스럽게 표현이 되야하지만 일반적인 Alpha Test 를 사용하게 되면 위와 같은 현상에 마주치게 된다. 이는 굉장히 끔찍한 현상이다. 실제 게임을 해보거나, 만들어본 사람이라면 안다. 대부분의 픽셀에 나무가 표현되고, 잎사귀들이 저런식으로 자글자글 거린다면 약간의 불쾌함이 느껴진다. VR 이라면 더욱..
그래서 급하게 대처방안으로 나온 것이 위 그림의 오른쪽에 나오는 Alpha to Coverage 라는 방법이다. 이는 하드웨어 MSAA 를 픽셀 쉐이더의 결과를 통해 자동으로 해주는것으로, MSAA 의 퍼포먼스와 비례한다. MSAA 는 성능이 영 좋지않아 안쓰는 경우가 꽤 많이 존재하기 때문에 Alpha to Coverage 는 절대적으로 사용할 수 있는 방법은 아니다. 게다가 엄청나게 많은 나무를 Alpha to Coverage 를 쓴다면.. 성능은 안봐도 뻔하다.
앞서 말한 Alpha Test 은 Material, Shader 별로 고정된 Alpha 값을 설정해 그 이하가 되면 Pixel Shader 에서 결과를 내놓지 않게 하는(Discard) 방법이였다. Alpha Test 의 문제는 샘플링한 Alpha 값이 가끔 극단적으로 낮아서 Discard 되는 것인데, 이를 간단하게 해결하기 위해 요상한 방법이 등장했다.
바로 Stochastic test 라는 방법이다.

위 그림에서 위쪽에 있는 것이 일반적인 Alpha Test 인데, color.a 는 텍스쳐에서 샘플링한 Alpha 값, ατ 는 Alpha Test 를 위한 고정된 Alpha Threshold(알파한계)다. 밑의 코드에서 drand48 이 나타내는 것은 단순한 0 ~ 1 사이의 랜덤값이다. 즉 랜덤하게 Alpha Threshold 를 설정해주어 물체가 멀어져서 평균 Alpha 값이 낮아질 때도 픽셀이 Discard 되지 않도록 하는 것이다. 하지만 이는 굉장한 눈아픔? 반짝거림? 을 유발한다. 범위를 지정해주지 않았기 때문에 이전 프레임에서 출력된 픽셀이 다음 프레임에서는 출력되지 않을 수도 있다. 이렇게 각 프레임마다 상황이 달라서 생기는 현상앞에 Temporal 을 붙인다. Stochastic Alpha Test 의 문제는 Temporal Flickering 이라고 할 수 있겠다.
Temporal Flickering 이 없는, Temporal Stability(임시적 안정성) 을 확보하기 위해서는 Alpha Threshold 를 이러저리 튀지 않게해야 했고, 이를 위해 특정 값에 따라서 Hash 값을 생성하는 방법이 고안되었다. 이 방법은 Hashed Alpha Test 라는 이름으로 작년에 공개되었다.
Hashed Alpha Testing
기본적으로 랜덤 값(난수) 생성은 제대로된 난수생성이 아닌, 특수한 식을 사용해서 의사 난수 생성 방법을 이용하는데, Hash 를 이용한 난수생성은 일반적으로 많이 쓰인다고 한다. Hashed Alpha Testing 은 Hash 를 생성하기 위한 Key 값을 선정하는데 조심스러웠다고 한다.
Key 로 선정될 수 있는 후보는 Texture Coordinate, World-Space Coordinate, Ojbect-Space Coordinate 이 세가지 였다고 한다. Texture Coordinate 는 가끔 없는 경우가 있어 제외하였고, World-Space Coordinate 는 정적 물체에는 원하는대로 동작하지만, 동적 물체의 경우에는 문제가 있었다고 한다. 결국 남은건 Ojbect-Space Coordinate 가 남게 되었다.
Ojbect-Space Coordinate 의 X,Y,Z 세 좌표를 모두 이용하게 되는데, 이는 X,Y 두개만 이용하게 되면 Hash 값이 Screen-Space 에서 생성되어 다른 물체와 겹치게 되면 Alpha to Coverge 같은 효과를 내게되어 3가지 좌표 모두 Hash 생성에 사용된다고 한다.
마지막으로 중요한 포인트는 Temporal Stability 를 확보하는 것이다. 이해하기 쉽게 설명하자면, 아래와 같은 각 픽셀을 나타내는 그리드안에 점이 있다고 가정해보자. 이 점들이 조금씩 움직여서 계속 픽셀안에 있다면, 같은 Hash 값을 사용하여 같은 Alpha Threshold 값을 만들어줘야 한다.
![]()
아래 두 그림의 빨간 점의 위치처럼 원래의 픽셀위치를 벗어나게 된다면 새로운 Alpha Threshold 를 생성해야 하겠지만, 위치가 많이 바뀌지 않는다면 같은 Alpha Threshold 를 사용해 Flickering 을 최대한 줄여야 한다.
![]()
이러한 맥락으로 Hashed ALpha Testing 은 Temporal Stability 를 조금 확보하게 된다. 물론 위의 그림은 이해를 돕기위한 용도로, 실제 코드상에서는 다른 방법을 통해 계산된다. 아래 코드를 보자.

위 코드는 픽셀이 가지고 있는 Object-Space Coordinate 의 옆 픽셀과의 차이, 세로에 있는 픽셀과의 차이를 통한 값으로 계산한다. (dFdX, dFdY 의 자세한 내용은 찾아보거나 What is ddx and ddy 에서 볼 수 있다.) 픽셀별로 값의 차이, 즉 근접한 픽셀의 위치 차이값에 따른값(미분값)과 그 값을 이용해 Object-Space Coordinate 값에 곱한 값을 Key 로 두어서 Alpha Threshold 를 계산한다.
마지막에 Alpha Threshold 를 구하는 코드를 보면, Floor 하는, 올림을 해주어 discrete value 로 Key 값을 넣어준다. Floor 가 의미하는 것은, 선형적인 데이터가 아닌 뚝뚝 끊기는 데이터로 만들어 특정한 값을 넘어야 Key 값이 바뀌게 하여 Hash 를 유지해 Flickering 을 방지하는 것이다. 아래 그림은 floor(x) 의 그래프다. 즉 코드의 pixScale 이 크면 클수록 Hash 의 값은 픽셀의 변화에 따라서 빠르게 바뀌고, 작으면 작을수록(0에 가까워질수록) 픽셀의 변화에 따라서 Hash 값이 느리게 바뀔 것이다.
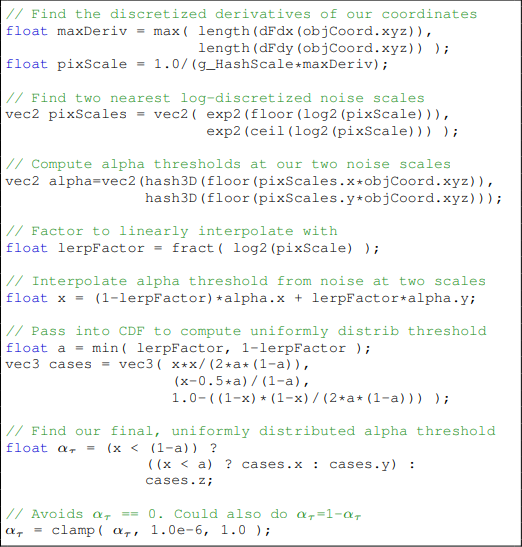
이러한 방법은 View-Space 를 기준으로 X,Y 좌표가 조금씩 바뀔때는 픽셀끼리의 차이를 계산하기 때문에 안정적이다. 하지만 Z(Depth) 값이 바뀔때는 많은 Flickering 을 일으킬 것이다. 이를 해결하기 위해 아래 코드를 보자.

위치의 픽셀별 차이 벡터의 크기를 discrete 시키는 방법도 좋은 아이디어중 하나다. 하지만 이는 빌보드처럼 큰 크기의 판이 다가오게 된다면 끝부분의 discontinuity 를 유발하게 된다.


그래서 위 코드와 같 discretize 시킨 올림처리한 값과, 내림처리한 값을 사용한 두 Hash 값 사이의 보간을 통해서 Alpha Threshold 를 구해준다. 하지만 이 코드는 아직 문제점이 존재한다. 만약 maxDeriv 의 값이 0 ~ 1 사이라면 내림값이 반드시 0이 되기 때문에 보간할 값 중 한개의 값이 고정되게 된다. 그래서 아래와 같은 코드를 사용한다.

pixScale 을 그냥 계산하는 대신, discretize 된 두개의 스케일값을 2의 지수로 표현하여 값이 0으로 되는 것을 막는다. 이렇게 보간된 값을 사용하여 Alpha Threshold 를 정해주면 약간의 문제가 생긴다. 보간을 함으로써 균일하지 않게 랜덤값이 분포되었기 때문이다. 그래서 아래와 같은 식을 사용하여 다시 값을 분포시켜준다.
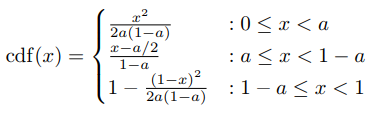
위의 식을 적용하면 모든 값들이 균일하게 분포되어 진정한 랜덤값의 Alpha Threshold 가 생성된다고 한다. 아래는 전체 코드다.
자세한 사항은 논문에서 확인할 수 있다([Cwyman17]). 결과는 아래 유튜브 영상에서 확인할 수 있다.
이를 통해 전보다 훨씬 나은 Alpha Test 품질을 얻을 수 있게 되었다. 하지만 Hashed Alpha Testing 의 결과는 Stochastic Test 처럼 픽셀이 흩뿌려진 느낌을 지울 수 없다. 어느정도의 랜덤값에서 생성이되니 이는 어쩔 수 없는 결과다.
Alpha Distribution
Alpha Test 의 구린 품질을 좀 더 개선할 수 있는 방법이 또 있다. 이번년도 I3D 에 제출된 Alpha Distribution 이라는 논문이 있는데, 이는 Hashed Alpha Testing 처럼 런타임에 계산을 하지않고 각 Mip-level 의 텍스쳐를 미리 처리해놓는 방법 중에 하나다. 미리 계산된 Texture 들을 사용하여 일반적인 Alpha Test 를 그대로 사용하기만 하면 된다. 아직 직접 사용한 예시는 없어 검증되지는 않았지만, 이 방법이 그대로 사용될 수 있다면 Alpha Test 부분에서는 거의 끝판왕이 될 것 같다.
Alpha Distribution 일반적인 Alpha Test 를 기준으로 Alpha Threshold 가 고정되어 있다는 것을 가정한다. 그렇게 되면 Alpha Threshold 에 따라서 픽셀에 출력이 되냐, 안되냐로 따질 수가 있다.(Binary Visibility) Binary Visibility 를 각 Mip-level 에 맞춰서 고르게 분산(Distribution)시키는게 Alpha Distribution 의 목적이다.
Alpha Distribution 은 두가지 분산방법을 사용한다. Error Diffusion 과 Alpha Pyramid 이라는 방법을 사용한다. 하나씩 알아보자.
Error Diffusion 은 하나하나의 픽셀을 순회하면서, 각 픽셀의 Binary Visibility 에 해당하는 값(0 아니면 1)과 이미지가 가지고 있는 Alpha 값을 비교해 그 오차(Quantization Error)를 다른 픽셀에 나누어준다. Binary Visibility 는 다음과 같이 정해진다.
αˆi = αi >= ατ : 1, αi < ατ : 0
αi 는 이미지가 가지고 있는 이산화된 Alpha 값이고, ατ 는 Alpha Threshold, 한계값을 뜻한다. αˆi 는 해당 픽셀의 Binary Visibility 를 뜻한다. 이것을 가지고 Quantization Error 를 계산한다.
ϵi = αi − αˆi
ϵi 는 Quantization Error 를 뜻하고 픽셀이 보이게 된다면 ~1 <= ϵi < 0 의 값을 가지게 되고 픽셀이 보이지 않는다면 0 < ϵi <= 1 의 값을 가지게 된다. 이런 Quantization Error 는 인근 픽셀로 분포된다. 아래 그림을 보자.
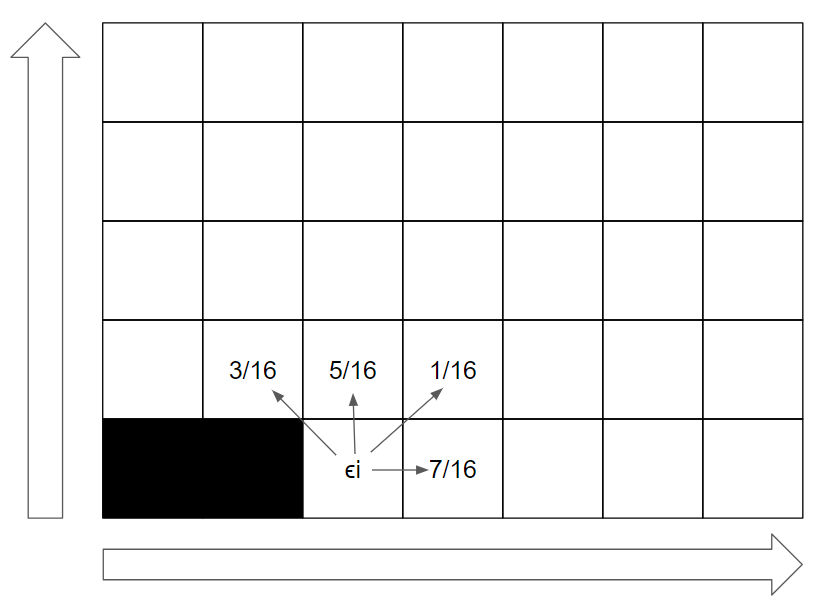
그림에서 ϵi 가 들어가 있는 부분이 현재 처리중인 픽셀이며, ϵi 의 값은 인근 픽셀로 고정된 비율로 Alpha 값에 더해진다. (x+1,y) 는 7/16, (x-1,y+1) 은 3/16, (x,y+1) 은 5/16, (x+1,y+1) 은 1/16 비율로 분포된다. 이런 방법으로 각 픽셀을 순회하면서 처리하면 Error Diffusion 은 간단하게 끝난다. 오차 확산이라는 이름이 굉장히 직관적이다.
Error Diffusion 은 픽셀과 픽셀사이의 Alpha 값을 고르게 분포시킨다. 하지만 약간의 문제가 존재한다. 보이게 되던, 안보이게 되던 Alpha 값이 0.3 ~ 0.7 정도로 중간값을 가지고 있다면, 한 픽셀은 강조되고, 옆의 픽셀은 보이지 않게 된다. 이러한 방법은 아래 이미지와 비슷한 결과를 만든다.
{: .center-image}
Error Diffusion 의 문제는 위 그림처럼 비슷한 색 영역에 있어도 분산된 영향을 받아서 각 픽셀이 부드럽게 보이지 않는 현상이 발생한다. 이러한 특징을 Dithering 이라고 부른다. 그래서 Alpha Distribution 논문에서는 이보다 나은 품질을 위해 Alpha Pyramid 라는 다른 방법이 소개된다.
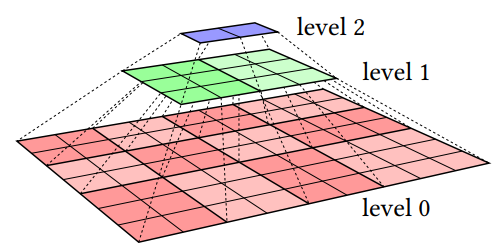
Alpha Pyramid 은 Error Diffusion 보다는 좀 더 복잡한 방식이다. Alpha Pyramid 라는 밉맵같은 개념의 텍스쳐들을 생성하고, 그 Alpha Pyramid 를 사용해서 Alpha 값들을 분산시키는 방법이다. Alpha Pyramid 를 만들고 값을 다루는 방법에 대해서 알아보자.
Alpha Pyramid 은 각각의 mip-level 마다 하나씩 생성된다. 즉 이미지 한개씩만 처리한다.
Alpha Pyramid 를 만들떄 맨 처음에 Mip-Map 과 비슷한 방식으로 Sub-level 들을 만든다. 맨 처음에 생성되는 level 의 해상도는 이미지 해상도의 1/4(1/2*1/2) 을 곱한 해상도로, 2의 지수가 아니여도 된다. 이렇게 생성된 level 1 은 약 원본 이미지의 해상도가 1/4이 되는데, level 0 의 각 픽셀들에 적어도 원본 이미지의 픽셀 4개의 알파값들을 더해서 저장한다. 원본 이미지의 해상도가 2의 지수가 아니라면 level 0 세로와 가로 끝부분의 픽셀들은 픽셀 6개의 알파값들을 더해서 저장하고, 가장 모서리의 픽셀 하나는 픽셀 9개의 알파값을 더해서 저장한다. 위의 이미지는 그리드로 원본의 해상도를 표시하고, 색으로 해당 레벨의 실질적인 픽셀들을 표시한다.
원본 이미지와 level 1 의 관계는 level 1 생성한 후 다음 Level 2 을 생성할 때 level 1 과 level 2 의 관계와 같다. 즉 같은 방법을 2x2 해상도가 될떄까지 계속 반복한다. 이렇게 생성된 Alpha Pyramid 의 각 레벨의 텍셀은 하위 레벨의 연관된 Alpha 값들의 합을 가지고 있는다. 이를 누적된 알파값(Accumulated Alpha)라고 부르겠다.
다음은 각각의 Accumulated Alpha 을 가지고 각각의 픽셀의 보여주는 여부를 결정하는 Visibility Value 를 구해야 한다. 처음에는 Alpha Pyramid 의 최상위 레벨의 각각의 Accumulated Alpha 값들의 합을 구하여 올림을 해준 값을 가지고 있는다. (이 값은 입력으로 들어온 이미지의 보여지는 픽셀을 정하는 값으로, 이 값이 하위 층으로 한층한층 분산되면서 결국 이미지의 보여지는 픽셀을 결정하게 된다. 논문에서는 텍스쳐 전체의 Visibility Value 라고도 한다.) Alpha Pyramid 의 최상위 레벨의 각각의 Accumulated Alpha 의 정수부의 값만(일반적으로 Alpha 값은 0 ~ 1 사이의 소수.) Visibility Value 에 저장한다. 그리고 각 Accumulated Alpha 의 소수부 값들 중 큰 값들만 Visibility Value 를 1씩 나누어준다. 이러면 모든 Visibility Value 가 분산된다. 이렇게 최상위 층의 처리가 끝난다.
그 다음 각각의 층들이 처리가 되야한다. 최상위 층은 각 Accumulated Alpha 을 가지고 있는 윗층이 없어 직접 구했지만, 아랫층부터는 상위 층들이 Accumulated Alpha 합을 구해서 가지고 있다. 이 값을 가지고 위에서 언급한 Visibility Value 를 계산하여 계속 구한다. level 1 까지 이 과정을 반복하면 Alpha Pyramid 내부에서 처리하는 과정은 끝난다.
다음은 마지막으로 계산된 Alpha Pyramid 의 최하층 level 1 의 Visibility Value 들과 맨 처음 입력으로 들어온 이미지를 처리한다. (위에서 Binary Visibility 에 대한 언급을 했었다. Alpha Test 의 이미지는 결국 보이냐, 안보이냐의 차이이기 때문에 Alpha Pyramid 도 level 1 의 Visibility Value 를 통해 이미지의 Binary Visibility 를 처리해준다.) level 1 에 관련된 2x2,2x3,3x2,3x3 픽셀의 Binary Visibility 를 처리한다. level 1 의 Visibility Value 의 값을 기존 이미지가 가지고 있는 Alpha 값이 큰 순서대로 1씩 나누어준다.(보이게 처리한다.) 그렇게 Visibility Value 를 다 쓰게되고 남아있는 픽셀들은 안보이게 처리한다.
Alpha Pyramid 는 순서대로 텍스쳐의 층을 쌓은 후 최상층에서 다시 차례대로 내려오면서 Visibility Value 를 분산시키고, 마지막으로 이미지의 각 픽셀의 Binary Visibility 를 정해주는 방법이다.
이 글에서의 Alpha Distribution 에 대한 내용은 논문 뿐만 아니라 논문의 저자가 제공한 코드까지 참조하여 썼다. 근데 논문의 내용중 여기서 언급하지 않은 내용이 있다. 저자가 제공한 코드에서는 Visibility Value 를 분산시킬 떄 소수부의 값이 큰 기준으로 분산시킨다. 하지만 논문에서는 이를 랜덤하게 처리한다고 한다. 왜냐하면 균일한 패턴의 생성을 막기 위해서라고 한다. 하지만 제공되는 코드에서는 랜덤하게 설정하는 부분은 없었다. 또한 코드에서는 Alpha Threshold 를 0.5 로 가정하여 코드를 짜놓아서
방법만 봐도 여러가지 이유로 Alpha Pyramid 이 Error Diffusion 보다는 더 나은 Alpha Test 를 제공할 것 같다는 생각이 든다. 논문에서도 실제로 더 나은 품질을 보여준다고 한다.
절대적으로 좋은 결과를 내게하는 방법은 없다. Alpha Distribution 역시 단점을 가지고 있다. 미리 처리를 하기 때문에 이미지가 고정되어 타일링처럼 보일 수가 있다. 또한 확대시 아무것도 처리하지 않고, Bilinear Filtering 만 걸은 것보다 안좋은 결과를 보여줄 수도 있다.

또 Alpha Threshold 가 고정되어 있다고 가정하기 때문에 값이 바뀌면 다시 계산해야한다. 직접 구현해서 붙이는 경우에는 계산하는 코드를 넣어주어야 하는데, 만약 Texture Compression 이 적용되어 있으면 굉장히 귀찮을 것이다. 거기에 상용엔진에 Intergration 할려면 더욱더 심할것이다.
그에 비해 Hashed Alpha Testing 은 구현하기엔 쉬운편이다. 코드는 Shader 에 붙여넣기만 하면 된다. 하지만 약간의 퍼포먼스를 잡아먹고, 뭉개진 가루처럼 보이는 현상이 존재하기 때문에 무조건 좋다고하기에는 무리가 있다.
조금더 시간을 가지고 지켜봐야 될것 같다는 생각이 든다.