What is Shadow Mapping 에서 Shadow Mapping 에 대한 간단한 번역 & 설명을 적어놓았다. 이번 글에서는 Shadow Mapping 을 효과적으로 사용하기 위한 Cascaded Shadow Mapping 에 대하여 적어보겠다.

Cascaded Shadow Mapping 을 구글 번역기에 돌려보면 “계단식 그림자 매핑” 이라고 나온다. 조금 직관적이지 않은 말이지만 뜻 자체는 맞다. 간단하게 Cascaded Shadow Mapping 에 대하여 말하자면 넓은 환경의 그림자를 위해 거리에(거의 Depth) 따라서 여러개의 Shadow Map 을 생성하는 방법이다.

넓은 범위의 Directional Light 가 닿는 그림자를 정확하게 표현하려면 꽤나 큰 크기의 Shadow Map 을 사용해야 한다. 하지만 Cascaded Shadow Mapping 을 사용한다면 여러개의 Shadow Map 을 사용하여 보다 조금의 메모리를 사용하여 넓은 범위의 그림자를 표현할 수 있다.

Shadow-map generation

Cascaded Shadow Mapping 을 위한 Shadow Map 생성은 앞서쓴 글에서 설명한 방법과 거의 유사하다. 앞서 여러개의 Shadow Map 을 생성하여 그림자를 표현한다고 언급했었다. 여러개의 Shaodw Map 을 생성하는 기준은 View frustum 을 Depth 를 기준으로 여러개로 쪼개어 각 쪼개진 frustum 을 기준으로 Shadow Map 을 그린다.

frustum 은 보통 Depth 값을 정하거나 어떤 알고리즘을 사용하여 쪼갠다. 이는 다음 포스팅에서 언급할 예정이다. frustum 을 쪼개주면 다음은 쪼개진 Camera View frustum 의 각각의 8개의 꼭지점들을 Light-Space 로 변환한다. 변환된 각각 꼭지점으로 2차원의 aligned axis bounding box 의 위치를 구해준다. 가장 작은 X,Y 값과 가장 큰 X, Y 값을 구해주면 된다.


출처 : NVidia : Cascaded Shadow Mapping


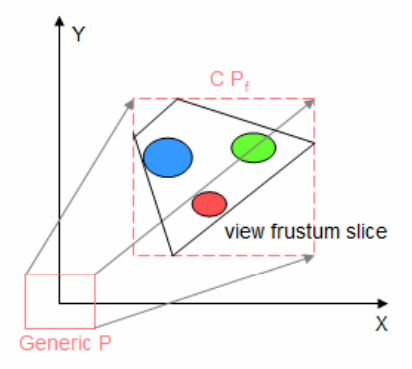
위 그림에서 XY 평면에서의 빨간색 선으로 되어있는 사각형이 언급한 aligned axis bounding box 를 말한다. 이 AABB 는 아래에서 특정한 행렬을 만들때 쓰인다.

NVidia : Cascaded Shadow Maps 에서는 이 Light-Space 로 변환하는 MVP 변환 에서 Projection 변환을 바꿔준다고 설명한다. 두개의 행렬이 나오는데, 하나는 직교 투영 행렬로(orthogonal projection) 나눠진 frustum 의 Far 값과 Near 값을 통해 생성해준다. 그리고 나머지 하나는 Crop Matrix 라는 변환 행렬이다.

위에서 구한 Light-Space 의 AABB 값을 통해 Crop Matrix 를 계산한다. 아래 그림에서나오는 Mx, My 와 mx, my 는 각각 Maximum X,Y, Minimum X,Y 를 뜻한다.


출처 : NVidia : Cascaded Shadow Mapping


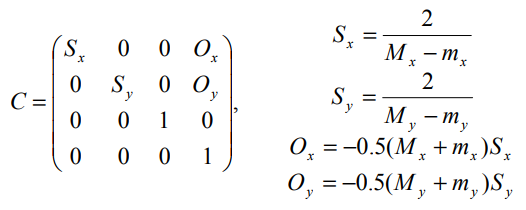
이렇게 계산된 Crop Matrix 의 역할은 해당 AABB 로 Shadow Map 이 그려질 범위를 결정해주는 역할을 한다. 다만 범위가 아주 정확하지는 않다. 아래 그림을 보자.


출처 : OGLdev : Cascaded Shadow Mapping


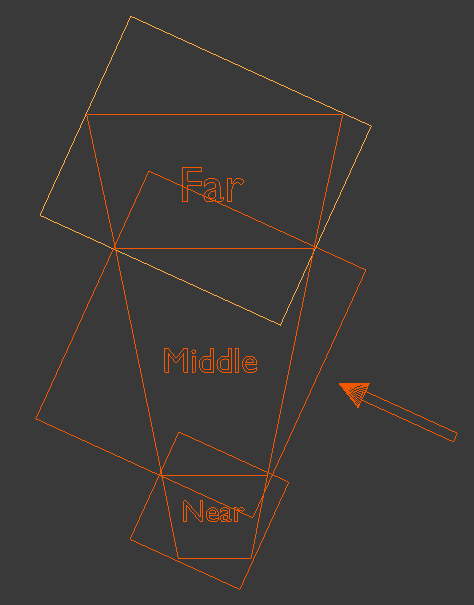
위 그림과 같이 보통은 겹치는 부분이 생긴다. 사용시에는 Depth 에 따라서 다르게 사용하기 때문에 크게 문제는 없다. 사용시에는 Depth 값에 따라서 다른 텍스쳐를 가져오는 것과 텍스쳐를 샘플링할때 UV 값을 정점의 위치를 Light-Space 로 변환해서 변환된 정점의 위치의 X,Y 좌표를 UV 값으로 사용하면 된다. 다만 각각의 Shadow Map 마다 변환 행렬은 Crop Matrix 때문에 다르기 때문에 따로 접근해야 한다.

자세한 사용법을 알고 싶으면 NVidia : Cascaded Shadow Map Example에서 소스를 받아 보면 된다.

추가

Cascaded Shadow Map 을 1 pass 로 그리는 방법은 간단하다. 우선 Shadow Map 들을 TextureArray 를 통해 저장하고, RenderTarget 을 Geometry Shader 에서 각각의 렌더타겟별로 지오메트리를 추가해주어 각각의 Pixel Shader 를 실행시키면 된다. 자세한 코드는 여기에서 볼 수 있다.

참조