Frustum Traced Shadow With Irrelgular Z Buffer 1
frustum Traced Shadow with Irregular Z-Buffer 0 에서 기법의 아이디어를 둘러봄으러써 대강 이 알고리즘이 무엇인지 살펴보았다. 이번 글에서는 논문에 수록된 포괄적인 전체 시스템과 복잡도에 대하여 알아볼 것이다.
전체 시스템
이전 글에서 두가지 단계에 대해서 자세한 설명을 했었다. Irregular Z-Buffer 를 생성하고 Visibility Test 를 하는 것이였다. 실제 구현된 단계는 총 6개의 단계로 이루어진다고 한다.
첫번째로는 Eye-Space Z-Prepass 를 해준다. 요즘의 엔진들이나 큰 규모가 아닌 게임이더라도 Z-Prepass1 는 거의 대부분 해준다. Geometry Pass 가 두번 걸리기는 하지만 Fill Rate 의 부하가 Geometry Pass 의 부하보다 많이 커서 그런 듯하다. 중요한건 단순히 언급한 Eye-Space Z-Prepass 를 뜻하는게 아니다. 이전에 언급한 μQuad 의 빠른 계산을 위해 G-Buffer 에 3개의 실수 값들을 넣는다. 이 3개의 실수는 실제 그려지는 카메라의 위치와 Tangent Plane 의 4개의 코너중에 3개의 거리를 나타낸다. 이는 μQuad 를 다시 계산하기에 충분하다고 한다.
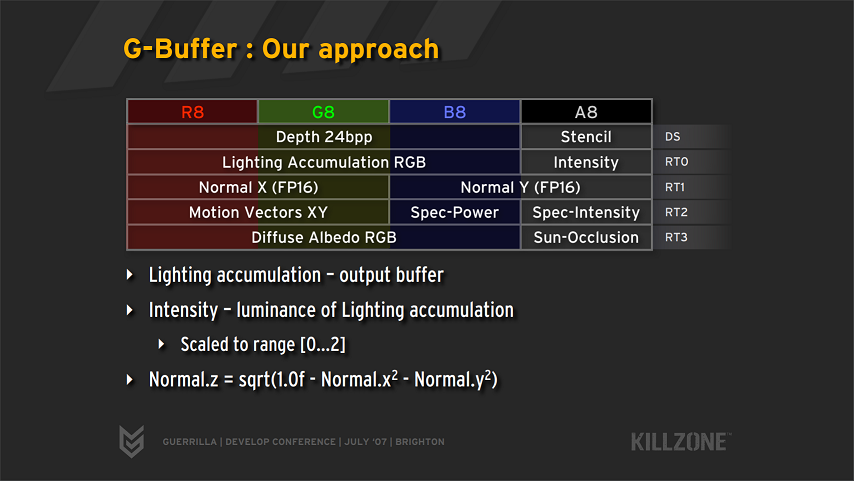
이 방법은 Visibility Test 의 속도를 빠르게 하는데 도움이 되지만, 당연히 G-Buffer 의 공간이 부족한 경우에는 쓰지 못한다. AAA 급의 게임들은 G-Buffer 를 bit 단위로 최대한 아껴쓰기 경우가 많기 때문에 이와 같은 상황이 일어날 수도 있다. 이런 경우에는 명시적으로 Visibility Test 를 할때 μQuad 를 계산한다고 한다. 아래 그림은 2009년에 발매된 KillZone 2 의 G-Buffer 사용을 나타내는 PT의 한 부분이다.
두번째로는 씬의 경계를 설정해주는 것이다. Shadow Mapping 에서 Light-Space Projection 행렬은 씬에 딱 맞게 해주어야 한다.2 딱 맞지 않는 경우에는 IZB 에 쓸모없는 텍셀을 생기게 하기 때문이다. 그래서 Light-Space Projection 행렬을 계산하기 위해 Compute Shader 와 Z-Buffer 를 사용하여 Bounding Box 를 계산한다. 이 계산은 화면의 해상도에 따라서 달라진다. 하지만 논문의 저자는 이 비용이 병목의 큰 원인이 아니기 때문에 특별한 해결 방법을 제시하지는 않는다.
세번째는 Irregular Z-Buffer 를 만드는 것이다. 이전 글에서 IZB 에 대한 대략적인 아이디어는 언급했었다. 더 디테일하게 이를 말해보면, 우선 Eye-Space Z Buffer 를 참조해 Light-Space 로 변환한 후에 Light-Space A-Buffer 의 텍셀의 Linked-List 에 넣는다.
IZB 의 발상은 Eye-Space 의 픽셀과 Light-Space 의 텍셀이 1:1 로 매칭되지 않고 하나의 텍셀이 참조당하는 횟수가 1을 넘을때 allasing 이 발생하는 것에서 시작되었다. 그래서 여기서 구현된 IZB 는 텍셀에 Linked-List 의 개념을 도입하여 보다 정확히 계산할 수 있게 하였다.
아래 그림은 IZB 의 데이터를 나타낸다.

왼쪽의 그림은 일반적인 Shadow Map 을 나타내고, 중간의 그림은 Linked-List 의 크기를 나타낸다. 흰색은 Linked-List 의 크기가 0인 텍셀을 나타내고, 검은색에 가까워질수록 Linked-List 의 크기가 점점 커지는 것을 나타낸다. 오른쪽의 그림은 필요없는 부분을 0으로 나타내고, 나머지 부분은 0 이상의 숫자를 나타내는 방식이다. 이는 아래에서 언급할 Light-Space Culling Prepass 에서 쓰인다.
픽셀별로 여러개의 가시성(가려진 정도)를 나타내는 픽셀은 여러개의 IZB Node 를 필요로 한다. 일반적인 Shadow Map 과는 다르게 μQuad 는 다른 Light-Space Texel 에 Projection 이 가능하다.
대충 생각해보면, N 개의 픽셀별 쉐도우가 필요하면, N 개의 IZB Node 가 필요하다. 하지만 쓸데없는 데이터를(Geometry 가 없는 경우) 넣지 않을 수 있으므로 M 개의 Light-Space Texel 에 μQuad 를 투영한다면, 우리는 min(N, M)개의 IZB Node 가 필요하다고 알 수 있다.
아래 그림은 IZB 를 사용하는 디테일한 구조를 나타낸다.
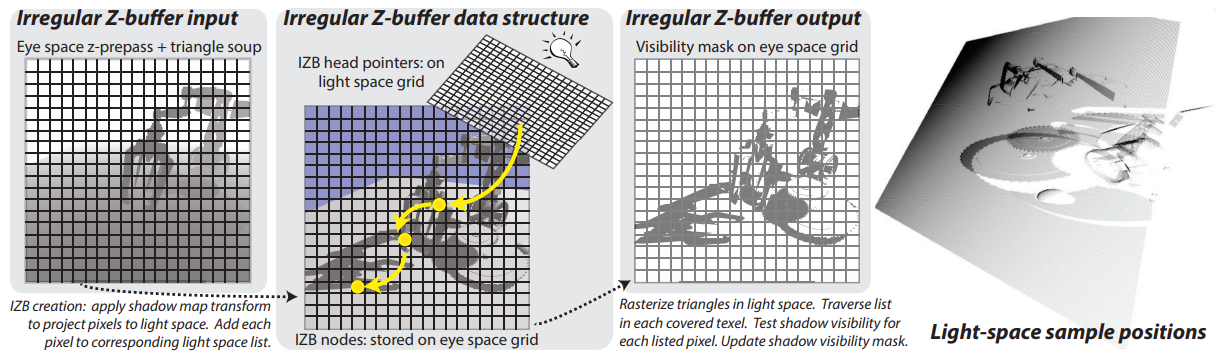
IZB 의 데이터 구조는 Light-Space A-Buffer : Eye-Space A-Buffer 의 Node 를 찾아가기 위한 데이터, Eye-Space A-Buffer : 리스트의 크기를 나타내는 버퍼와 같다. 출력되는 결과 : Visibility Buffer 또한 따로 존재한다. 이게 최종적으로 그려질때 사용된다.
다음은 Light-Space Culling Prepass 다. Visibility Test 를 위해 Geometry 의 Light-Space Conservative Rasterization 을 하게 되는데, GPU 에서 Early-Z 기능을 제공한다면 쓸데없는 부분(아무것도 없는 텍셀, 가장 끝)을 컬링할 수 있다.
하지만 Early-Z 하드웨어를 사용할때는 Light-Space Z-Buffer 를 필요로 한다. 이는 조금 당황스러운 상황을 만든다. 그래서 이 단계에서는 반드시 스텐실 버퍼를 만들어야 한다. 위에서 언급한 쓸데없는 부분(아무것도 없는 텍셀, 가장 끝)의 Depth 를 0으로 세팅한다. 나머지는 0 이상의 숫자로 세팅한다.
논문의 저자에 따르면, 엄청 큰 씬을 제외하고는 30% ~ 50% 의 성능 향상을 보였다고 한다. 이는 Conservative Rasterization 으로 생성된 Fragment 의 절대적인 숫자를 줄이고, 아무것도 없는 리스트를 스킵하면서 길이의 다양성을 없엔 효과다.
컬링을 된 이후에는 픽셀별로 Visibility Test 를 해준다. 이때 각각의 폴리곤들은 임의의 텍셀 집합을 가리기 된다. 그리고 각각의 텍셀이 가진 리스트를 순회하면서 Visibility Test 를 한다. 이때 atomic OR 을 사용하여 Visibility Buffer 에 기록한다. 여기서 가장 병목이 되는 구간은 각각의 폴리곤이 임의의 서로다른 길이를 가진 텍셀의 리스트를 커버링하여 각각의 쓰레드별로 실행되는 시간이 제각각이 된다. 문제는 시간이 제각각인 경우, 가장 느린 시간을 소모한 쓰레드를 기준으로 divergence 하여 각각의 텍셀의 리스트의 길이 중 가장 긴 길이의 시간으로 맞춰진다. 이는 최악의 상황을 유발할 수 있다.
마지막으로 Visibility Buffer 를 사용하여 실제 오브젝트들을 렌더링하면 된다.
복잡도 계산
위에서도 언급햇다시피 이 기법은 N 번의 Visibility Test 한다면, 시간 복잡도는 O(N) 과 같다. 여기서 N 을 분해하면 다음과 같다. O(La * F), F 는 Light-Space 의 Fragment 갯수이고, La 는 Linked-List 의 평균 길이다.
La 또한 다른 요소로 나타낼 수 있다. Visibility Test 는 Eye-Space 에서 한다. 그래서 IZB Node 의 갯수는 Eye-Space 의 해상도에 비례한다. 그리고 Eye-Space 의 데이터는 전부 Light-Space 에 기록되므로 La ≈ (Eye-Space Resolution) / (Light-Space Resolution) 으로 계산될 수 있다.
하지만 위에서 언급했던 것과 같이 SIMT 기반의 GPU 에서는 O(La * F) 가 아닌 O(Lm * F) 이 될 수 밖에 없다. Lm 은 Linked-List 의 최대 길이다. 결국 퍼포먼스를 내기 위해선 Lm 의 길이를 줄이는 것이 가장 중요하다는 것이 된다.
이번 글에서는 전체 시스템과 복잡도에 대해서 알아보았다. 다음은 더 디테일한 구현 부분의 내용을과 Alpha 처리에 대한 부분을 알아볼것이다.